“Americas most easterly observatory”
“Americas most easterly observatory”
PROJECT DOUBLE STARS
Stars--What Are They Like?
Distances---Trigonometric Parallax
Unlike the other sciences, astronomy is entirely observational. You cannot run experiments on things. You cannot manipulate the objects to see how they work. In order to compare the objects you see from the Earth, you must first know how far away they are. Obviously, you cannot use a tape measure or send spacecraft out to the stars and measure how far they travelled. Bouncing radar off the surfaces of stars would not work because: (1) stars are glowing balls of hot gas and have no solid surface to reflect the radar beam back and (2) the radar signal would take years to just reach the nearest stars.
A favorite way to measure great distances is a technique used for thousands of years: look at something from two different vantage points and determine its distance using trigonometry. The object appears to shift positions compared to the far off background when you look at it from two different vantage points. The angular shift, called the parallax, is one angle of a triangle and the distance between the two vantage points is one side of the triangle. Basic trigonometric relations between the lengths of the sides of a triangle and its angles are used to calculate the lengths of all of the sides of the triangle. This method is called trigonometric parallax. Modern surveyors use this method to measure great distances, so the method is sometimes called ``the surveyor's method''.
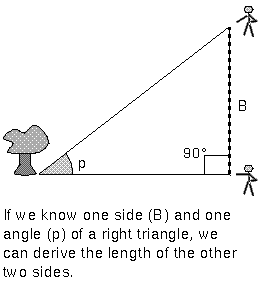
The side of the triangle between the observers, labelled ``B'' in the figure above, is called the baseline. The size of the parallax angle p is proportional to the size of the baseline. If the parallax angle is too small to measure because the object is so far away, then the surveyors have to increase their distance from each other. Ordinarily, you would have to use trigonometric functions like a tangent or a sine, but if the angle is small enough, you find a very simple relation between the parallax angle p, baseline B, and the distance d:
where the angle p is measured in the tiny angle unit called an arc second. The farther away the object is, the less it appears to shift. Since the shifts of the stars are so small, arc seconds are used as the unit of the parallax angle. There are 3,600 arc seconds in just one degree. The ball in the tip of a ballpoint pen viewed from across the length of a football field is about 1 arc second.
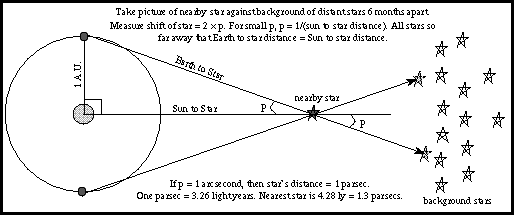
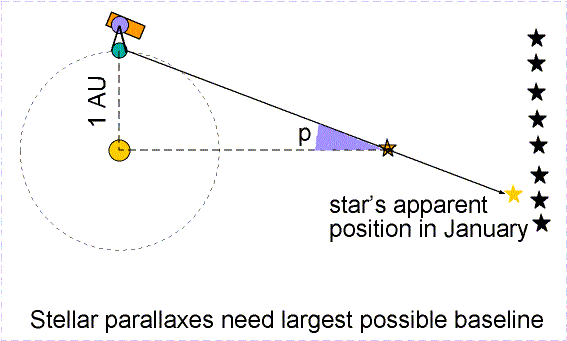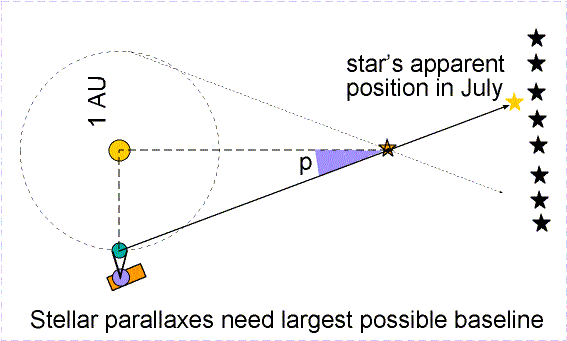
Trigonometric parallax is used to measure the distances of the nearby stars. The stars are so far away that observing a star from opposite sides of the Earth would produce a parallax angle much, much too small to detect. As large a baseline as possible must be used. The largest one that can be easily used is the orbit of the Earth. In this case the baseline is the distance between the Earth and the Sun---an astronomical unit (AU) or 149.6 million kilometers! A picture of a nearby star is taken against the background of stars from opposite sides of the Earth's orbit (six months apart). The parallax angle p is one-half of the total angular shift.
However, even with this large baseline, the distances to the stars in units of astronomical units are huge, so a more convenient unit of distance called a parsec is used (abbreviated with ``pc''). A parsec is the distance of a star that has a parallax of one arc second using a baseline of 1 astronomical unit. Therefore, one parsec = 206,265 astronomical units. The nearest star is about 1.3 parsecs from the solar system. In order to convert parsecs into standard units like kilometers or meters, you must know the numerical value for the astronomical unit---it sets the scale for the rest of the universe. Its value was not know accurately until the early 20th century (see the planetary science chapter). In terms of light years, one parsec = 3.26 light years.
Which unit should you use to specify distances: a light year or a parsec? Both are fine and are used by astronomers (including myself) all of the time, just as you may use ``feet'' and ``yards'' in everyday talk. However, when the parsec unit is used on this web site, the equivalent in light years will usually be given as well, but when the light year unit is used, the parsec equivalent will usually not be given. Using a parsec for the distance unit and an arc second for the angle, our simple angle formula above becomes extremely simple for measurements from Earth:
Parallax angles as small as 1/50 arc second can be measured from the surface of the Earth. This means distances from the ground can be determined for stars that are up to 50 parsecs away. If a star is further away than that, its parallax angle p is too small to measure and you have to use more indirect methods to determine its distance. Stars are about a parsec apart from each other on average, so the method of trigonometric parallax works for just a few thousand nearby stars. The Hipparcos mission greatly extended the database of trigonometric parallax distances by getting above the blurring effect of the atmosphere. It measured the parallaxes of 118,000 stars to an astonishing precision of 1/1000 arc second (about 20 times better than from the ground)! It measured the parallaxes of 1 million other stars to a precision of about 1/20 arc seconds. Selecting the Hipparcos link will take you to the Hipparcos homepage and the catalogs.
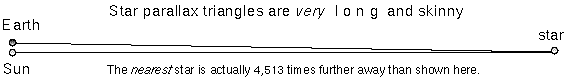
The actual stellar parallax triangles are much longer and skinnier than the ones typically shown in astronomy textbooks. They are so long and skinny that you do not need to worry about which distance you actually determine: the distance between the Sun and the star or the distance between the Earth and the star. Taking a look at the skinny star parallax triangle above and realizing that the triangle should be over 4,500 times longer (!), you can see that it does not make any significant difference which distance you want to talk about. If Pluto's entire orbit was fit within a quarter (2.4 centimeters across), the nearest star would be 80 meters away! But if you are stubborn, consider these figures for the planet-Sun-star star parallax triangle setup above (where the planet-star side is the hypotenuse of the triangle):
| the Sun--nearest star distance = | 267,068.230220 AU = | 1.2948 pc; |
| the Earth--nearest star distance = | 267,068.230222 AU = | 1.2948 pc; |
| Pluto--nearest star distance = | 267,068.233146 AU = | 1.2948 pc! |
If you are super-picky, then yes, there is a slight difference but no one would complain if you ignored the difference. For the more general case of parallaxes observed from any planet, the distance to the star in parsecs d = ab/p, where p is the parallax in arc seconds, and ab is the distance between the planet and the Sun in AU.
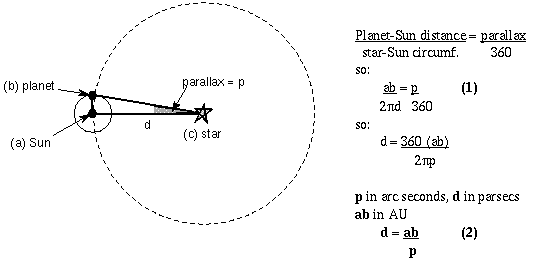
Formula (1) relates the planet-Sun baseline distance to the size of parallax measured. Formula (2) shows how the star-Sun distance d depends on the planet-Sun baseline and the parallax. In the case of Earth observations, the planet-Sun distance ab = 1 A.U. so d = 1/p. From Earth you simply flip the parallax angle over to get the distance! (Parallax of 1/2 arc seconds means a distance of 2 parsecs, parallax of 1/10 arc seconds means a distance of 10 parsecs, etc.)
A nice visualization of the parallax effect is the Distances to Nearby Stars and Their Motions lab (link will appear in a new window) created for the University of Washington's introductory astronomy course. With this java-based lab, you can adjust the inclination of the star to the planet orbit, change the distance to the star, change the size of the planet orbit, and even add in the effect of proper motion.
Vocabulary
| astronomical unit | parsec | trigonometric parallax |
|---|
Formulae
- small angle relation: angle p in arc seconds = (206,265 × B)/d. The baseline B and distance d must be in the same units of length.
- star parallax relation: parallax angle p in arc seconds = B / d. The baseline B is in units of A.U. and the distance d is in units of parsecs. For measurements from the Earth, B = 1.
- star distance d = B / p. For measurements from the Earth, B = 1.